3.4 Reaktivität und Reaktorperiode

Für einen stabil kritischen Reaktor wurde definiert, dass der Multiplikationsfaktor k = 1 ist. Nun können bestimmte Umstände dazu führen, dass der Reaktor k = 1 verlässt und einen anderen Wert für k annimmt.

Als Mass für die Abweichung von k = 1 bzw. k_inf = 1 bzw. k_eff = 1 hat man dieReaktivität definiert. Sie ist in ihrer Aussage dem gleich, was der Multiplikationsfaktor beschreibt: Den Zustand der Kritikalität bzw. die Stabilität der Kettenreaktion.

Die Reaktivität r ist definiert zu:

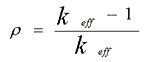
Allgemein gibt man sie in Prozent an.
Definitionsgemäss gelten folgende Beziehungen für Reaktivität und Multiplikationsfaktor:

r = 0 entspricht k_eff= 1, der Reaktor ist kritisch
r < 1 entspricht k_eff < 1, der Reaktor ist unterkritisch
r > 1 entspricht k_eff> 1, der Reaktor ist überkritisch

Die Reaktivität ist stark von dem Betriebszustand des Reaktors als auch von bestimmten Eigenschaften, den Reaktivitätskoeffizienten, verschiedener Materialien abhängig.
Diese Faktoren, die die Reaktivität beeinflussen, werden in der Reaktivitätsbilanz berücksichtigt.

Für die Fahrweise eines Reaktors ist die Grösse "Reaktivität" natürlich auch bedeutsam:
Wird mehr Leistung benötigt, macht man den Reaktor überkritisch. In der Praxis fährt man dazu die Steuerstäbe aus dem Kern bzw. (speziell im Siedewasserreaktor) erhöht man den Systemdruck.

Dieses darf aber nur in gewissen Grenzen geschehen. Die obere Grenze ist in diesem Falle beta, also der Anteil verzögerter Neutronen im Kern. Es darf also theoretisch die Reaktivität im Reaktor nur so stark erhöht werden, dass rho < beta. Formuliert drückt diese Bedingung aus, dass der Reaktor "verzögert überkritisch" ist. Würde rho > beta sein, so wäre der Reaktor "prompt überkritisch" - das bedeutet, dass alleine die prompten Neutronen schon den überkritischen Zustand herbeiführend würden. Dass hiesse, dass beispielsweise bei einer Reaktivität von rho = beta + 0,01 die Anzahl der Kettenreaktionen in nur 0,1 Sekunden auf das 10^21-fache steigen würde! Dieser Zustand muss natürlich vermieden werden, da die Regelsysteme des Reaktors sonst Schwierigkeiten bekämen.

In der Praxis steigert man in U-235-Reaktoren zur Leistungserhöhung die Reaktivität um max. 0,1%. Beta hat den Wert 0,65%. Man ist somit also deutlich unterhalb der Grenze. Die Leistung des Reaktors wird auch in diesem Falle erhöht - es dauert lediglich etwas länger.

Die Reaktorperiode:

Die Reaktorperiode T_p ist eine Kenngröße die beschreibt, in welcher Zeit sich der Neutronenfluss (Anzahl freier Neutronen, die in 1 Sekunde eine Fläche von 1 Quadratzentimeter durchsetzen, also das Produkt von Neutronenanzahl und deren mittlere Geschwindigkeit) um den Faktor e (Eulersche Zahl e = 2,72...) ändert. Sie ist positiv bzw. negativ wenn der Neutronenfluss steigt bzw. sinkt. T_p geht gegen unendlich, wenn der Neutronenfluss konstant ist.
Berechnen lässt sich die Reaktorperiode durch folgende Formel:

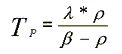
Darin sind die Grössen "Reaktivität", "Anteil der prompten Neutronen an der Gesamtzahl der Neutronen im Kern" sowie die "Zerfallskonstante der betrachteten Spaltprodukte", im Mittel ist diese 0,08 1/sec.

In realen Reaktoren liegt T_p bei etwa 69 - 71 sec., da dort mit Reaktivitäten von etwa 0,1% im gearbeitet wird.

(Sascha Greinke)